미적분 문항들의 풀이를 시작해 보자. 수열의 극한 부터 미분법까지의 범위로 시험이 치뤄진 만큼 주요 문제들을 미분법의 내용들이 출제되었다. 다양한 미분 방식들에 대한 평가와 역함수의 미분계수(28번) 등이 출제되었다.

23번 문항
1보다 작은 수들의 무한대 거듭제곱이 등장한다. 이런 극한의 문항은 분모, 분자에 2의 n제곱이나 3의 n제곱을 동시에 곱해서 정리해보면 바로 그 해답이 나오는 경우가 대부분이다. 2점짜리 문제인 만큼 절대 틀리지 말자.
24번 문항
미분법이 범위에 포함되었으니 당연히 간단한 문제로든 어려운 문제로든 음함수의 미분법이 나올 수 밖에 없다. y를 x의 식 덩어리로 인식하고 식을 잘 미분하면 된다. 헷갈린다면 y를 f(x)로 바꾸고 그 식을 미분해보면 더 직관적으로 이해가 쉽다.

25번 문항
급수가 수렴한다는 것은 당연히 안에 있는 수열을 0으로 수렴한다는 것을 의미한다. 이 내용을 모르면 절대 안된다.
26번 문항
극한 문항이 그래프와 연계되어 나왔다. 삼각형의 넓이 이므로 밑변, 높이를 잘 설정하고 식으로 표현하면 된다. 수식에서 ln(1+5t), ln(1+t) 와 같은 수식이 등장했으니 당연히 어떤 형식의 극한식이 만들어질지 예상되어야 하겠다. 분모분자를 잘 정리해서 답을 도출해 보자.
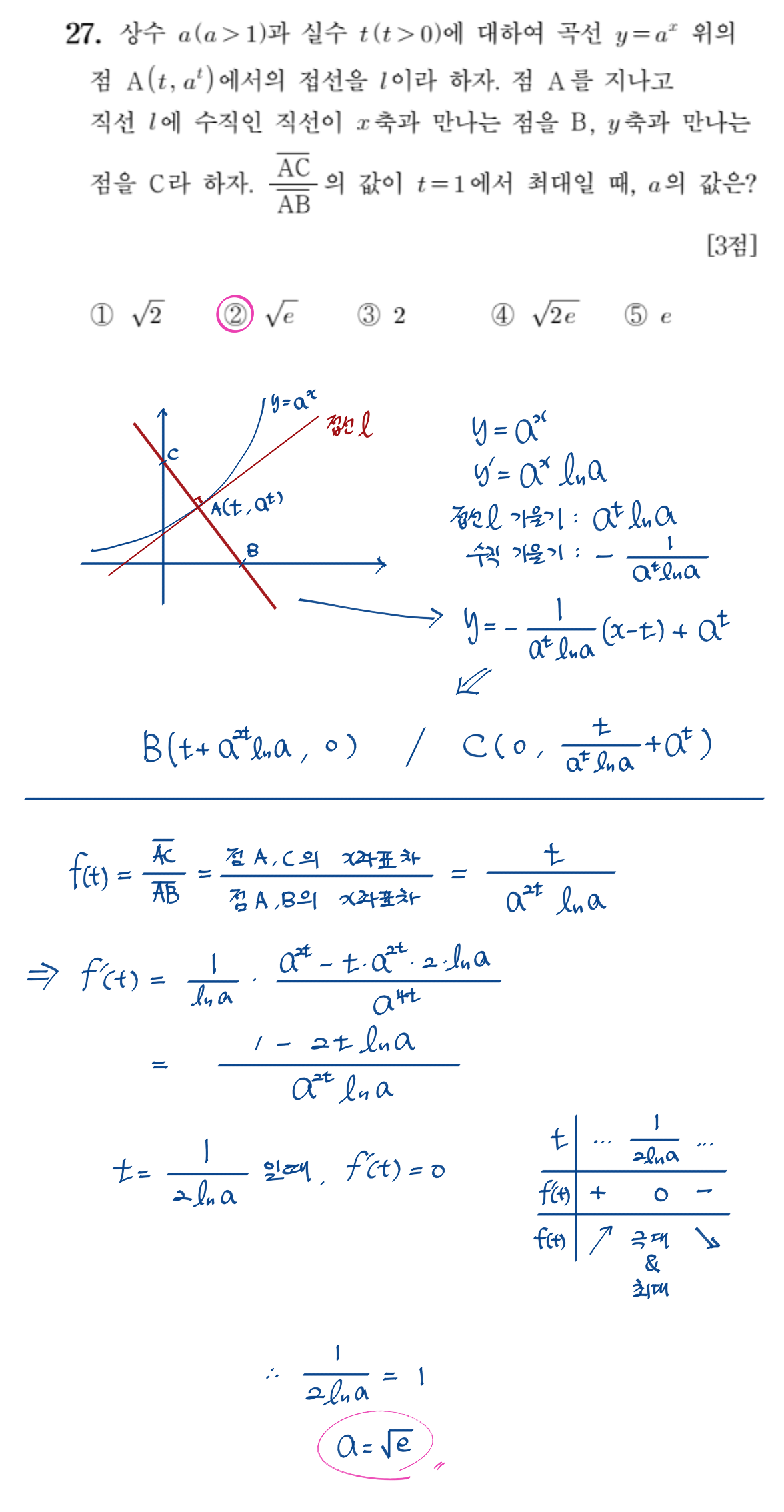
27번 문항
3점짜리 문항치고는 조금 어려운 느낌일 수도 있겠다. 접선과 수직인 직선을 긋고 x절편, y절편을 찍어서 길이 비율까지 잡아야 하니 조금 귀찮다. 하지만 길이비율을 x좌표 끼리의 비율이나 y좌표 끼리의 비율로도 쉽게 표현이 가능하니 잘 살펴보자. 모든걸 구한 다음에도 또 미분을 해서 최대가 되는 상황을 판단해야 하니 확실히 3점짜리 치고는 문제의 과정이 길다. 다양한 개념들을 하나의 문항에서 동시에 평가한다는 부분에서는 괜찮은 문제라고 하겠다.
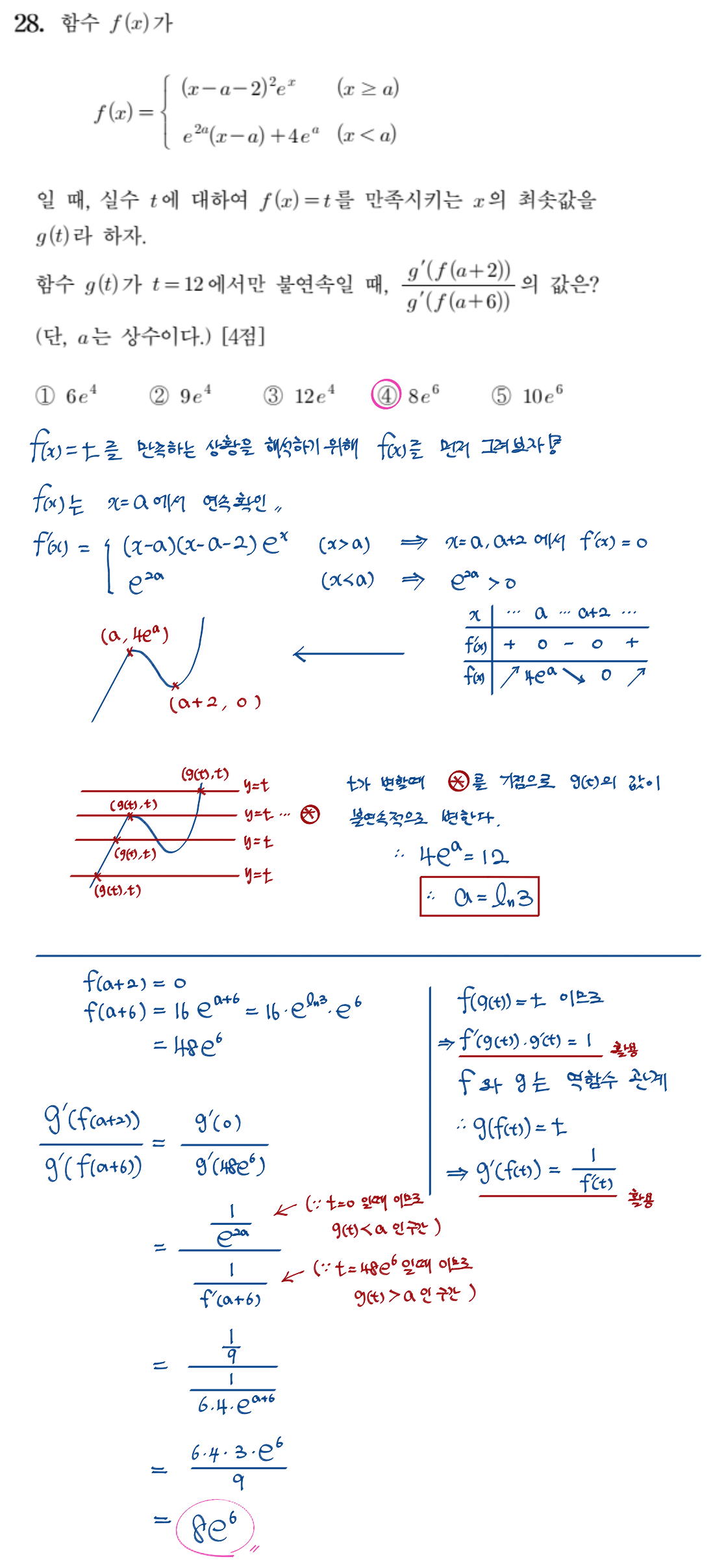
28번 문항
미적분에서 최고난이도 2개 문항 중 하나다. a의 값을 모르지만 사실 그래프는 매우 쉽게 그려지는 편이다. 하지만 f(x)=t를 만족하는 최소의 x값을 g(t)로 둔다는 이런 설정을 처음보는 입장에서는 생소하고 어렵게 느껴질 수 밖에 없다. 매년 다양한 문제들을 수능특강, 수능완성, 모의고사에서 접하는 필자의 경우는 위와 같은 형식의 문제를 너무 여러번 기출에서 접해보았기 때문에 바로 파악이 가능하지만 기출을 접해보지 못한 학생들에게는 상당히 어렵게 다가올 것이다. 풀이를 잘 보고 해석해보자. 이 문제에서의 가장 중요한 부분 두 곳은 f(g(t))=t 임을 알고 역함수의 대응관계임을 활용할 수 있어야 하는 포인트 , g'(0) 의 값은 직선구간에서의 기울기 역수임을 잘 해석하는 것이 포인트 이다.

29번 문항
f(x)를 미분해서 도함수를 찾아보면 f(x)의 기울기가 0보다 크거나 같다는 것을 판단할 수 있는데 이것을 ②조건에만 활용하는 순간 b, c의 값이 찾아지기 때문에 갑자기 문제가 쉽게 풀려 버린다. 도함수는 반드시 정리해서 해석까지 해야하게 때문에 만약 도함수가 분수와 다항식이 섞여 나온다면 반드시 통분해서 정리 해야한다.
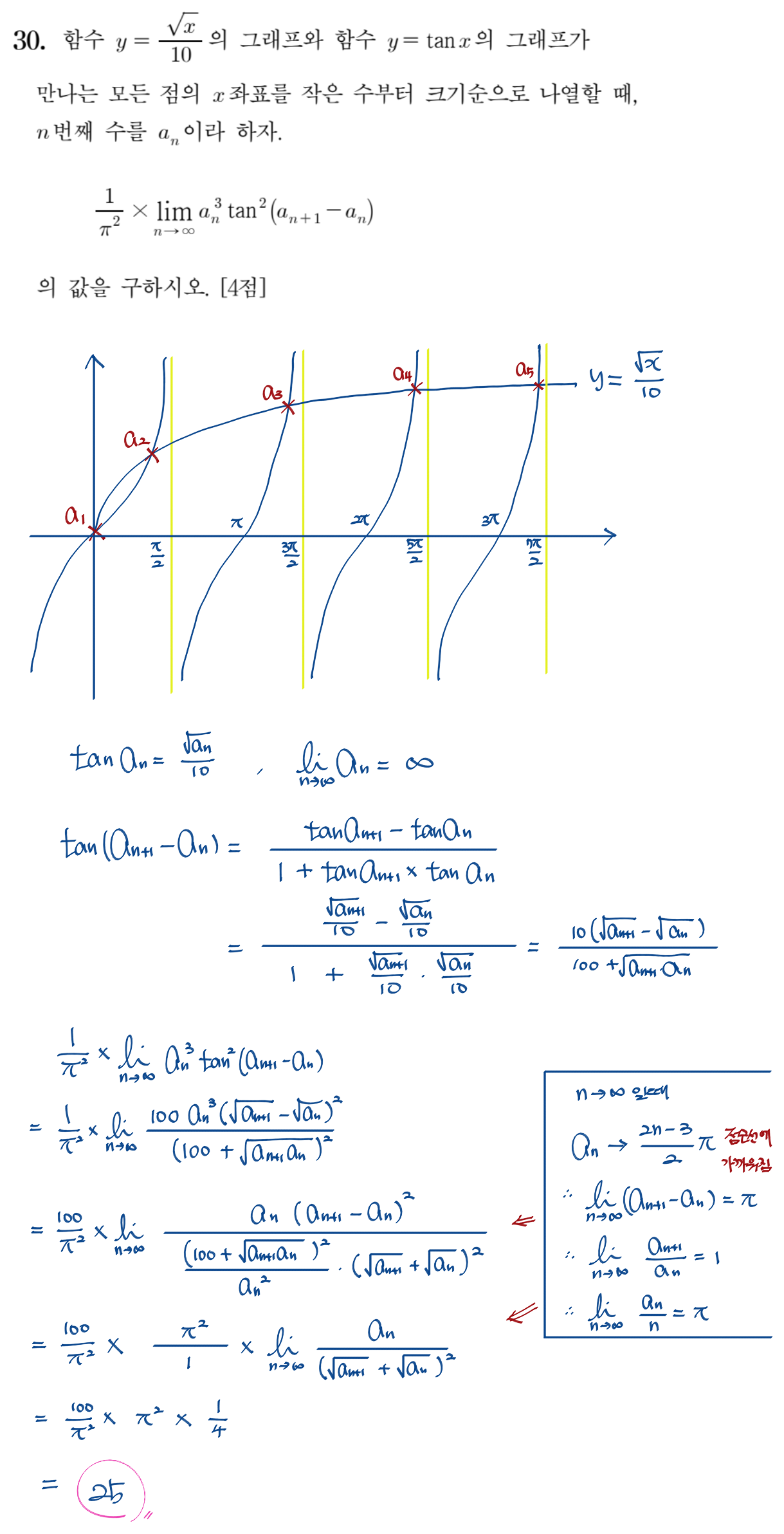
30번 문항
미적분 최고난도 마지막 문항이다. 무리함수와 tan함수의 교점을 수열화 시키고 이를 적용한 수열의 극한 문항을 제시하였다. 다항함수, 삼각함수, 지수함수, 로그함수, 유리함수, 무리함수 이런 다양한 형식의 함수들이 섞여서 방정식을 만들면 절대 수식으로 평범하게 풀리지 않는다..... 물론 종종 희한하게 정리가 되도록 수식을 만들어 놓은 경우도 있지만 일반적으로는 다양한 수식이 섞이면 방정식이 안풀리고 식으로 정리가 안된다.... 그렇다면 수식의 정리가 아닌 방향성이나 범위의 식으로 해석할 수 밖에 없는 특수한 상황이 생기는데 이를 활용한 문항이다. 우리는 딱딱 떨어져서 정리되고 값이 나오는 식과 답을 좋아하기 때문에 이러한 문항을 잘 다루지 못하는 경우가 많고 일단 기출도 많지 않다. 반드시 다시 풀어보고 다양한 풀이방식을 고민해보고 찾아보길 권한다.
이것으로 미적분 선택영역의 6월 모의평가 풀이를 마친다.
다음 포스팅을 확률과 통계 선택영역 풀이를 진행하도록 하겠다.
2025학년도 수능대비 6월 모의평가 수학 확률과통계 손풀이 23~30번 (2024년 6월 모의평가)
2025학년도 수능대비 6월 모의평가 수학 확률과통계 손풀이 23~30번 (2024년 6월 모의평가)
확률과 통계 문항들의 풀이를 시작해 보자. 확률단원까지의 내용들이 범위에 포함되었고 당연히 중요하게 출제되는 조건부 확률, 중복조합 등의 다양한 경우의 수 문항들이 등장하였다. 난이도
openmath.tistory.com
'수학 공부방 > 고3 6, 9월 모의평가' 카테고리의 다른 글
| 2025학년도 수능대비 9월 모의평가 수학 손풀이 공통 1~10번 (2024 9월 모평) (0) | 2024.09.12 |
|---|---|
| 2025학년도 수능대비 6월 모의평가 수학 확률과통계 손풀이 23~30번 (2024년 6월 모의평가) (0) | 2024.06.13 |
| 2025학년도 수능대비 6월 모의평가 수학 손풀이 16~22번 (2024년 6월 모의평가) (0) | 2024.06.11 |
| 2025학년도 수능대비 6월 모의평가 수학 손풀이 11~15번 (2024년 6월 모의평가) (0) | 2024.06.11 |
| 2025학년도 수능대비 6월 모의평가 수학 손풀이 1~10번 (2024년 6월 모의평가) (0) | 2024.06.11 |



