11번 부터 15번 까지의 고난도 문항에 대한 풀이를 살펴보자.

11번 문항
삼차함수 f(x)의 다양한 정보가 나와 있다. 천천히 하나씩 정리해서 수식으로 만들어 놓자. 접선의 y절편 정보도 있으니 접성의 방정식도 만들어야 할것이고 극한 정보도 수식으로 만들어보자. 정보가 쌓였다면 그다음 단계는 f(x)를 수식으로 찾는 것인데 바로 계수들을 만들수 없다면 필자의 방식대로 계수들을 문자로 설정하고 주어진 정보들을 대입하여 계수를 찾아내는 방식으로 하면 무난하게 웬만한 문항들을 풀어낼 수 있다.

12번 문항
지수함수의 점들을 활용해 도형의 넓이를 구하는 문항이다. 당연히 길이들의 값들이 필요하니 모르는 위치를 표현해야한다. 점A와 점C의 x좌표를 따로 잡은 것은 식이 너무 복잡해질 것으로 판단되었기 때문이다. 그냥 하나의 문자를 써도 상관은 없겠다. 길이의 조건을 활용해 방정식을 풀고 하나하나씩 위치들을 잡아보자. 계산은 조금 귀찮아도 풀이를 보면 알겠지만 풀만하다.
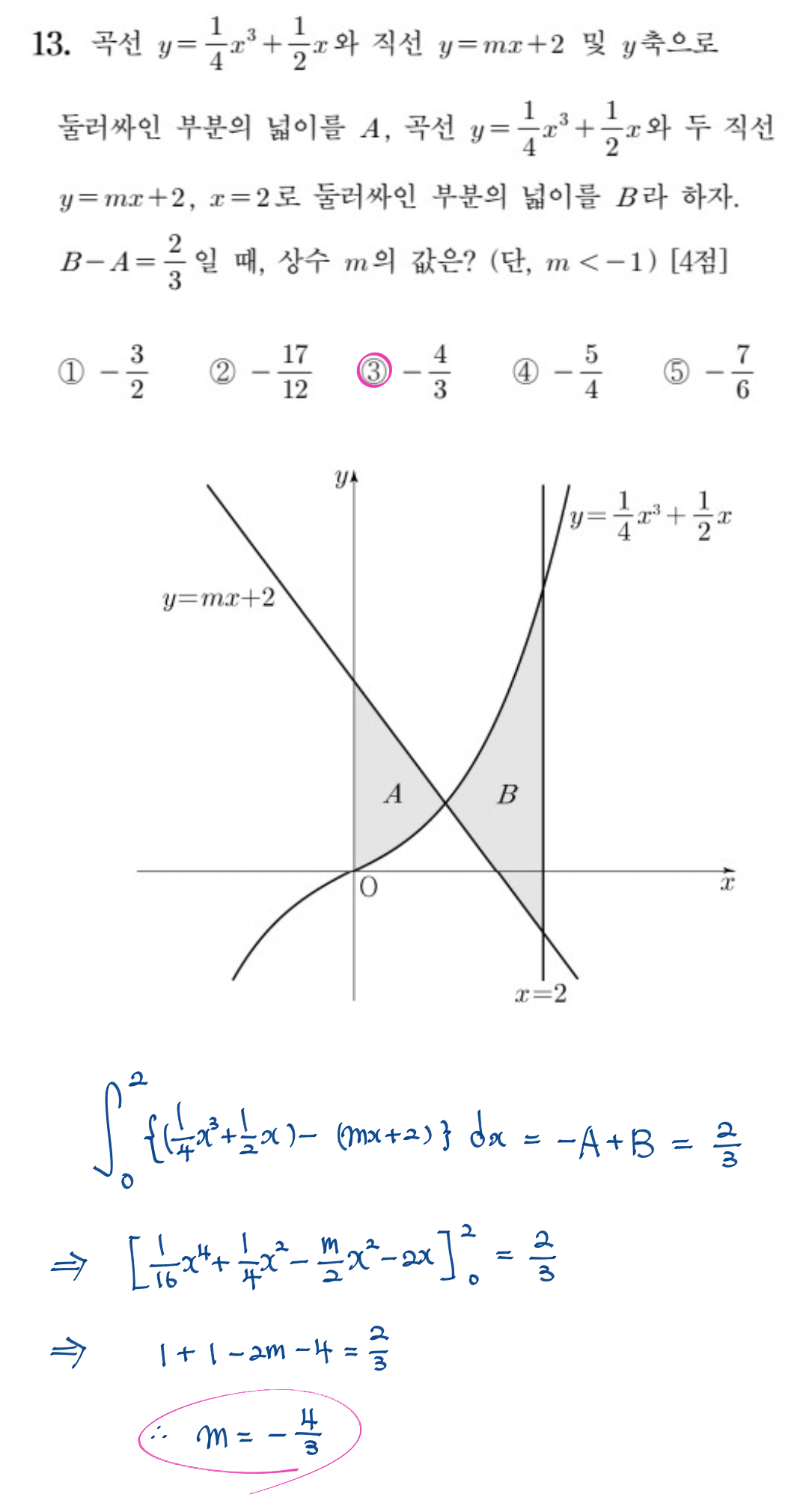
13번 문항
너무 쉬운 정정분 문항이 등장했다. 13번 위치는 그래도 조금 어려울 법도 한데.... 어쨌든 A넓이와 B넓이의 차를 주었으니 0부터 2까지의 전체구간에서의 정적분을 한방에 써도 되는 상황이 되었다. 두 함수가 교차해서 그려지므로 한쪽은 음의 정적분 값, 한쪽은 양의 정적분 값이 나오지 자연스럽게 조건의 값을 바로 쓸 수 있다. 이런 기술적인 내용은 반드시 알아야 한다. 두 구간을 나누어 정적분 하기 시작하면 매우 귀찮고 복잡한 식의 전개가 될것이 뻔하다.

14번 문항
진수조건과 부등식을 동시에 만족시키는 상황을 찾아내는 문항이다. 동시에 만족해야하는 부등식이 3개나 되기 때문에 귀찮지만 각각의 상황에 12개의 만족하는 상황이 등장하도록 몇번의 과정을 거쳐야 모든 답을 찾을 수 있다. 킬러 문항을 없앤다고 하더니...... 귀찮은 퀴즈가 늘어나는 느낌이 되었다. ;;;;;;
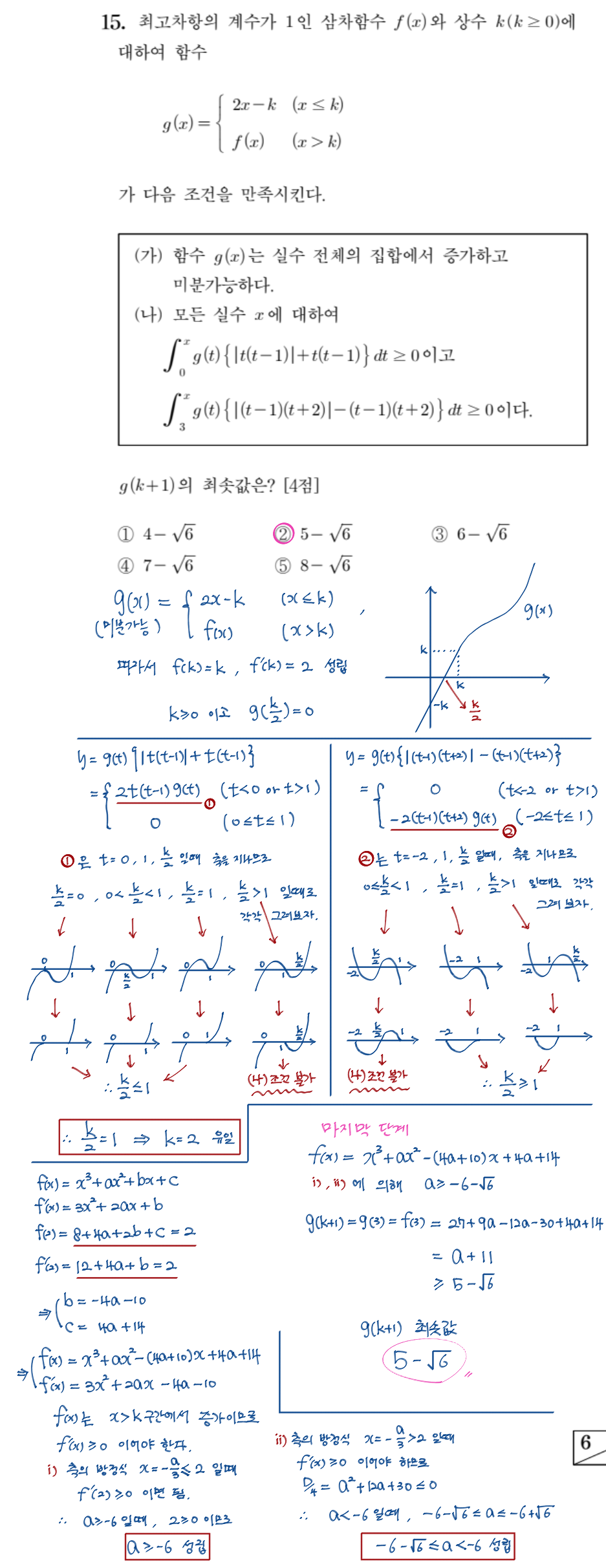
15번 문항
공통 객관식 마지막문항으로 객관식 중 가장 난이도가 높다. 미분가능과 증가함수의 조건을 활용해 일단 f(x)의 정보를 구하더라도 그다음 스텝으로 할 수 있는 것이 없고 (나) 조건을 해석하지 못하면 풀 수 없는 문항이다. (나) 조건에서 절댓값이 있는 구간과 그 옆의 수식이 동일함을 인지하고 범위에 따라 0의 값이 등장하는 것을 본다면 필자처럼 범위를 나누어 수식을 분리해야겠다는 생각을 할 수 있겠다. 머리속에 박아두어야 하는 절댓값에 대한 생각은 당연히 제곱해서 절댓값을 없애거나 범위를 분리해서 절댓값을 풀어내는 2가지의 방법이다. 그리고 나서 g(x)가 x축을 지나는 지점이 k/2로 유일한 것을 활용해 여러 경우를 분리하고 만족하는 상황을 찾아내면 된다. 마지막 증가함수의 조건을 만족하는 a의 범위를 구하는 것 까지 상당한 시간이 소요되는 문항이다. 킬러 문제를 내지 않겠다고 하더니 문제의 과정을 너무 길게 뽑아버렸다. 물론 좋은 문제이긴하다. ㅎㅎㅎ;;;;
다음 포스팅은 16번 부터의 주관식 문항이다.
2025학년도 수능대비 6월 모의평가 수학 손풀이 16~22번 (2024년 6월 모의평가)
2025학년도 수능대비 6월 모의평가 수학 손풀이 16~22번 (2024년 6월 모의평가)
16번 부터 22번 까지 서논술형 고난도 문항까지 살펴보자. 16번 문항 17번 문항 18번 문항 19번 문항 20번 문항 21번 문항 22번 문항 다음 포스팅은 미적분 선택영역의 풀이를 진행하
openmath.tistory.com
'수학 공부방 > 고3 6, 9월 모의평가' 카테고리의 다른 글
| 2025학년도 수능대비 6월 모의평가 수학 미적분 손풀이 23~30번 (2024년 6월 모의평가) (0) | 2024.06.11 |
|---|---|
| 2025학년도 수능대비 6월 모의평가 수학 손풀이 16~22번 (2024년 6월 모의평가) (0) | 2024.06.11 |
| 2025학년도 수능대비 6월 모의평가 수학 손풀이 1~10번 (2024년 6월 모의평가) (0) | 2024.06.11 |
| 2024학년도 수능대비 9월 모의고사 수학 손풀이 확률과 통계 28,29,30번 (2023년 9모, 9월 모평) (0) | 2023.09.07 |
| 2024학년도 수능대비 9월 모의고사 수학 손풀이 미적분 28,29,30번 (2023년 9모, 9월 모평) (0) | 2023.09.07 |



